Actividad 9
ACTIVIDAD
1. ¿Que es la Tecnologia Digital y para que se utiliza?
2. Realiza un listado de artefactos y productos que esten basados en tecnologia digital
3. ¿Que es el Sistema Binario y cuales son sus aplicaciones?
4. ¿Cual es la forma de convertir del sistema decimal al sistema binario, de binario a decimal, de binario a optal, de optal a binario, de binario a exadecimal y exadecimal a binario?
5. En el Cuaderno de Tecnologia crear un mapa conceptual que visualice la Tecnologia Digital, cuales son sus caracteristicas y aplicaciones, y otro mapa que visualice que es el sistema binario, cuales son sus aplicaciones y las conversiones que pueden hacer en los diferentes tipos de sistema con un ejemplo.
SOLUCION
1. ¿Que es la Tecnologia Digital y para que se utiliza?
Un sistema digital es un conjunto de dispositivos destinados a la generación, transmisión, manejo, procesamiento o almacenamiento de señales digitales. También, y a diferencia de un sistema analógico, un sistema digital es una combinación de dispositivos diseñados para manipular cantidades físicas o información que estén representadas en forma digital; es decir, que sólo puedan tomar valores discretos.
Para el análisis y la síntesis de sistemas digitales binarios se utiliza como herramienta el álgebra de Boole.
sistemas digitales combinacionales: Aquellos cuyas salidas solo dependen del estado de sus entradas en un momento dado. Por lo tanto, no necesitan módulos de memoria, ya que las salidas no dependen de los estados previos de las entradas.
sistemas digitales secuenciales: Aquellos cuyas salidas dependen además del estado de sus entradas en un momento dado, de estados previos. Esta clase de sistemas necesitan elementos de memoria que recojan la información de la 'historia pasada' del sistema.
Para la implementación de los circuitos digitales, se utilizan puertas lógicas (AND, OR y NOT), construidas generalmente a partir de transistores. Estas puertas siguen el comportamiento de algunas funciones booleanas.
Según el propósito de los sistemas digitales, se clasifican en: a) sistemas de propósitos especiales y b) sistemas de propósitos generales. Estos últimos permiten el cambio de su comportamiento mediante la programación de algoritmos de soluciones de problemas específicos. La mayoría de las computadoras modernas (año 2016) son sistemas digitales de propósito general.
2)
-Calculadora : el sistema se encuentra en la pantalla la cual muestra resultados u operaciones matematicas descritas

-microondas: el sistema muestra el tiempo programado para calentar un alimento

-Reloj: el sistema muestra en la pantalla la hora,minutos e incluso segundos y microsegundos (algunos como por ejemplo relojes de mano)

-cronometro: este sistema muestra o mide el tiempo desde un principio hasta un punto final descrito

-Termometro: es el sistema que mide el calor o clima del ambiente

-bascula: es el sistema digital que muestra los gramos o kilos de algun alimento

-DVD: es el sistema digital que reprduce y asu ves muestra el tiempo que dura una pelicula,documental o video

3)El sistema binario, llamado también sistema diádico1 en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los sistemas que se utilizan en las computadoras, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).2
Aplicaciones:En 1937, Claude Shannon realizó su tesis doctoral en el MIT, en la cual implementaba el Álgebra de Boole y aritmética binaria utilizando relés y conmutadores por primera vez en la historia. Titulada Un Análisis Simbólico de Circuitos Conmutadores y Relés, la tesis de Shannon básicamente fundó el diseño práctico de circuitos digitales.
En noviembre de 1937, George Stibitz, trabajando por aquel entonces en los Laboratorios Bell, construyó una computadora basada en relés —a la cual apodó "Modelo K" (porque la construyó en una cocina, en inglés "kitchen")— que utilizaba la suma binaria para realizar los cálculos. Los Laboratorios Bell autorizaron un completo programa de investigación a finales de 1938, con Stibitz al mando.
El 8 de enero de 1940 terminaron el diseño de una "Calculadora de Números Complejos", la cual era capaz de realizar cálculos con números complejos. En una demostración en la conferencia de la Sociedad Estadounidense de Matemática, el 11 de septiembre de 1940, Stibitz logró enviar comandos de manera remota a la Calculadora de Números Complejos a través de la línea telefónica mediante un teletipo. Fue la primera máquina computadora utilizada de manera remota a través de la línea de teléfono. Algunos participantes de la conferencia que presenciaron la demostración fueron John von Neumann, John Mauchly y Norbert Wiener, quien escribió acerca de dicho suceso en sus diferentes tipos de memorias en la cual alcanzó diferentes logros.
El sistema binario se aplica para todos microprocesadores. El sistema binario es lo q utiliza el computador para almacenar todo tipo de información como:
Imágenes-Textos-Juegos
Programas Las telecomunicaciones también son aplicaciones del sistema binario, ya que estas manejan demasiada información y es mucho más fácil almacenarla. Las redes también son aplicaciones del sistema binario porque a la igual q las telecomunicaciones manejan demasiada información a nivel mundial y es más fácil y organizado hacerlo atreves de "0" (cero) y "1" (uno). Tal vez nos preguntaremos ¿cómo se convierte la informacion a sistema binario? pues esto lo hace automáticamente el computador, pues está programado para almacenar la información.
Ejemplo
El sistema binario puede ser representado solo por dos dígitos. Un número binario puede ser representado por cualquier secuencia de bits (dígitos binarios), que suelen representar cualquier mecanismo capaz de usar dos estados mutuamente excluyentes. Las siguientes secuencias de símbolos podrían ser interpretadas como el mismo valor numérico binario:
1 0 1 0 0 1 1 0 1 0 | - | - - | | - | - x o x o o x x o x o y n y n n y y n y n
Aporte personal: Esto es un sistema importante y para lo que son sistemas operativos y muchas mas sistemas informaticos.
4)Decimal a binario:
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Este será el número binario que buscamos.
Ejemplo
Transformar el número decimal 131 en binario. El método es muy simple:
131 dividido entre 2 da 65 y el residuo es igual a 1
65 dividido entre 2 da 32 y el residuo es igual a 1
32 dividido entre 2 da 16 y el residuo es igual a 0
16 dividido entre 2 da 8 y el residuo es igual a 0
8 dividido entre 2 da 4 y el residuo es igual a 0
4 dividido entre 2 da 2 y el residuo es igual a 0
2 dividido entre 2 da 1 y el residuo es igual a 0
1 dividido entre 2 da 0 y el residuo es igual a 1
R//:Ordenamos los residuos, del último al primero: 10000011
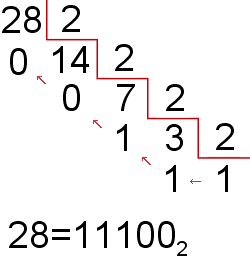
-Binario a decimal
Para realizar la conversión de binario a decimal, realice lo siguiente:
1:Comience por el lado derecho del número en binario. Multiplique cada dígito por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 20).
2Después de realizar cada una de las multiplicaciones, súmelas todas y el número resultante será el equivalente al sistema decimal.
Ejemplos:(Los números de arriba indican la potencia a la que hay que elevar 2)

-Sistema binario a octal
Debido a que el sistema octal tiene como base 8, que es la tercera potencia de 2, y que dos es la base del sistema binario, es posible establecer un método directo para convertir de la base dos a la base ocho, sin tener que convertir de binario a decimal y luego de decimal a octal. Este método se describe a continuación:
Para realizar la conversión de binario a octal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
|
Número en binario |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Número en octal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
3) La cantidad correspondiente en octal se agrupa de izquierda a derecha.
Ejemplos
·110111 (binario) = 67 (octal). Proceso:
111 = 7
110 = 6
Agrupe de izquierda a derecha: 67
· 11001111 (binario) = 317 (octal). Proceso:
111 = 7
001 = 1
11 entonces agregue un cero, con lo que se obtiene 011 = 3
Agrupe de izquierda a derecha: 317
·1000011 (binario) = 103 (octal). Proceso:
011 = 3
000 = 0
1 entonces agregue 001 = 1
Agrupe de izquierda a derecha: 103

-Octal a binario
Cada dígito octal se convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
Ejemplo
· 247 (octal) = 010100111 (binario). El 2 en binario es 10, pero en binario de 3 bits es Oc(2) = B(010); el Oc(4) = B(100) y el Oc(7) = (111), luego el número en binario será 010100111.

-Binario a hexadecimal
Para realizar la conversión de binario a hexadecimal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
|
Número en binario |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
Número en hexadecimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.

-Hexadecimal a binario
Note que para pasar de Hexadecimal a binario, se remplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario

5)mapa: Mapa binario y digital.pptx (119940)



